Sigma-AlgebraDefinition  -Algebra -Algebra
Universität
Ein System 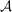 von Teilmengen einer Menge von Teilmengen einer Menge 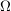 heißt eine heißt eine  -Algebra (in -Algebra (in 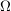 ), wenn es folgende Eigenschaften besitzt: ), wenn es folgende Eigenschaften besitzt:
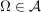 ; ;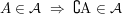 ; ;- für jede Folge
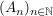 von Mengen aus von Mengen aus 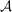 liegt liegt 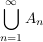 in in 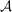 . .
Zum Vergleich siehe Ring, Algebra, Dynkin-System
"Duale" Eigenschaften einer  -Algebra -Algebra
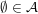 - für jede Folge
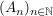 von Mengen aus von Mengen aus 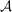 liegt liegt 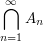 in in 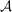
Beispiele von  -Algebren: -Algebren:
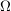 beliebige Menge: beliebige Menge: 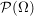 (dabei (dabei 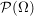 Potenzmenge von Potenzmenge von 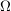 ) )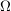 beliebige Menge: beliebige Menge: 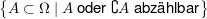 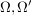 Mengen, Mengen, 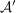  -Algebra in -Algebra in 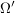 , , 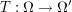 Abbildung: Abbildung: 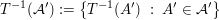 ist ist  -Algebra -Algebra
Quelle: isbn3110136252
|