TeilermengeDie Teilermenge einer Zahl n ist die Menge aller Zahlen, die ein Teiler von n sind, z.B.
Formale Definition:
Eigenschaften der Teilermenge:
- Die Zahl 1 ist in jeder Teilermenge enthalten:
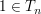 für alle für alle 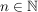
- Falls n>1, so ist n ebenfalls in ihrer Teilermenge enthalten:
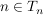 für alle n>1. für alle n>1.
- Eine Zahl
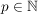 ist prim, wenn ihre Teilermenge genau zwei Elemente besitzt: ist prim, wenn ihre Teilermenge genau zwei Elemente besitzt: 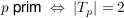
- Der größte gemeinsame Teiler (ggT) der Zahlen n und m ist das größte Elemente in der Schnittmenge der Teilermengen:
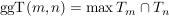
Siehe auch ggT, kgV, Vielfachenmenge
|