TangensDefinition Tangens und Tangensfunktion
Schule
Betrachtet man das unten stehende rechtwinklige Dreieck ABC mit dem rechten Winkel bei C (Bild1),
so gelten folgende Beziehungen:
{picture file=img/wiki_up//RechtwinkligesDreieck.jpg}
Dabei nennt man die Strecke 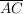 die Ankathete zum Winkel die Ankathete zum Winkel 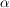
und die Strecke 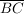 die Gegenkathete zum Winkel die Gegenkathete zum Winkel 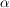 . .
{picture file=img/wiki_up//Einheitskreis.png}
Den tan-Wert liest man ab, indem man am Einheitskreis den Winkel abträgt und diese schräge Strecke verlängerst bis zu der vertikalen Gerade bei x = 1.
Die Länge dieser vertikalen Strecke (grüne Strecke) ist der tan-Wert.
Der tan-Wert ist einheitenfrei, d.h. ohne Einheit (so wie sin und cos auch).
Lediglich der Winkel 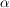 wird i.a. im Gradmaß und x im Bogenmaß angegeben. wird i.a. im Gradmaß und x im Bogenmaß angegeben.
weitere Überlegungen zu Sinus- und Kosinusfunktion
Aus der Definition des Tangens ergibt sich unmittelbar die zugehörige Funktion, bei der x im Bogenmaß angegeben wird:
{picture file=img/wiki_up//tangens.jpg}
Ebenso ergeben sich die weiteren Eigenschaften der Tangensfunktion:
- die Tangensfunktion ist an den Nullstellen der Kosinusfunktion nicht definiert:
- Wertebereich: alle reellen Zahlen
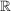
- die Tangensfunktion ist periodisch mit der Periodenlänge
 . .
- die Tangensfunktion ist über den gesamten Definitionsbereich betrachtet nicht symmetrisch,
- wohl aber, wenn man sich auf ein Intervall zwischen zwei Unstetigkeitsstellen einschränkt,
- dann ist sie punktsymmetrisch zu ihrer Nullstelle, insbesondere über dem Intervall
![$ [-\bruch{\pi}{2};\bruch{\pi}{2}] $ $ [-\bruch{\pi}{2};\bruch{\pi}{2}] $](/teximg/4/3/00388134.png) symmetrisch zum Ursprung. symmetrisch zum Ursprung.
Ableitung der Tangensfunktion
ergibt sich aus der Definition 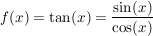 mit Hilfe der Quotientenregel: mit Hilfe der Quotientenregel:
Stammfunktion der Tangensfunktion
Universität
Definition/Darstellung als Potenzreihe
Für 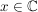 (insbesondere für (insbesondere für 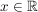 ) ist definiert (Taylorreihe des Tangens): ) ist definiert (Taylorreihe des Tangens):
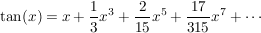
Bild1 Rechtwinkliges Dreieck aus ![Link auf "http://de.wikipedia.org/wiki/Sinus" [link]](/images/popup.gif) Wikipedia Wikipedia
weitere Überlegungen zu Sinus- und Kosinusfunktion
|