Funktionsuntersuchung1Untersuche die Funktion f mit
Da f eine ganzrationale Funktion ist, ist der Definitionsbereich die Menge aller reellen Zahlen: 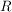 . .
Man kann zeigen, dass alle ganzrationalen Funktionen stetig sind; daher wird dieser Punkt i.a. nicht gesondert hervorgehoben.
Zu prüfen ist, ob eine der beiden Bedingungen für die Symmetrie einer Funktion vorliegen:
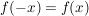 , denn dann ist die Funktion achsensymmetrisch zur y-Achse,
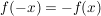 , denn dann ist die Funktion punktsymmetrisch zum Ursprung
Wenn keine dieser Bedingungen erfüllt ist, liegt keine Symmetrie im o.a. Sinne vor.
Man kann leicht zeigen, dass für alle ganzrationalen Funktionen folgende leichter zu prüfenden Bedingungen gelten:
wenn der Funktionsterm von f nur gerade Exponenten enthält, dann gilt: 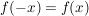 : f ist achsensyymetrisch.
wenn der Funktionsterm von f nur ungerade Exponenten enthält, dann gilt: 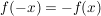 : f ist punktsyymetrisch.
bei 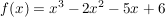 kommen gerade und ungerade Exponenten vor kommen gerade und ungerade Exponenten vor 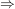 keine der o.a. Symmetrien liegt vor. keine der o.a. Symmetrien liegt vor.
4. Verhalten im Unendlichen
Zu prüfen ist das Verhalten der Funktion für große x:
Man erkennt das Verhalten besonders leicht, wenn man im Term die höchste vorkommende Potenz von x ausklammert:
Für große x nähert sich der Wert in der Klammer offensichtlich dem Wert 1; lediglich der Term 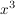 bestimmt das Verhalten von f: Es gilt: bestimmt das Verhalten von f: Es gilt:
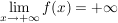 und 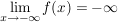
Dies gilt für alle ganzrationalen Funktionen mit einem ungeraden höchsten Exponenten.
Ist der höchste Exponent gerade, so gilt:
Liegt der Funktionsterm bereits als Produkt von "kleineren" Faktoren vor, so gilt der Satz vom Nullprodukt, man kann daher die Nullstellen unmittelbar ablesen.
Andernfalls versucht man den Term durch Polynomdivision zu faktorisieren.
Hier liest man unmittelbar ab: 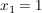 , , 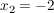 , , 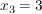
Zum Ableiten benutzt man den ausmultiplizierten Term und wendet die Ableitungsregeln an:
liefert die Kandidaten für die Extremstellen (notwendige Bedingung).
Man löst die Gleichung mit der p-q-Formel oder der ABCFormel:
Nachweis der hinreichenden Bedingung:
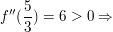 Tiefpunkt und
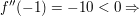 Hochpunkt
Die y-Koordinaten der beiden Punkte ermittelt man, indem man 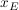 in den Term f(x) einsetzt: in den Term f(x) einsetzt:
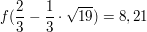 und und 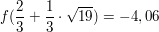
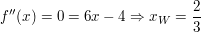 (notwendige Bedingung) (notwendige Bedingung)
da 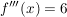 für alle x größer als 0 ist, liegt tatsächlich eine Wendestelle vor: Wendepunkt für alle x größer als 0 ist, liegt tatsächlich eine Wendestelle vor: Wendepunkt 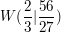
9. Skizze
|